Eratosthène de Cyrène

La mesure de la circonférence terrestre

Si Aristote définit la Terre comme une "sphère de modeste dimension", d'autres savants grecs se sont intéressé au calcul de cette dimension.

1. Eratosthène de Cyrène (-284 à -192)

Au sujet de la grandeur de la Terre, de très nombreuses opinions ont été émises parmi les physiciens, mais celles de Posidonius et d'Eratosthène sont supérieures aux autres. ... Celle d'Eratosthène procède de la géométrie et a la réputation d'être un peu plus obscure. Mais son exposé deviendra clair si nous partons des présupposés suivants : supposons

• en premier lieu, que Syène et Alexandrie sont situées sous le même méridien.
• deuxièmement, que la distance entre ces deux villes est de cinq mille stades.
• troisièmement, que les rayons projetés de différentes parties du Soleil sur différentes parties de la Terre sont parallèles : les géomètres supposent, en effet, qu'ils le sont.

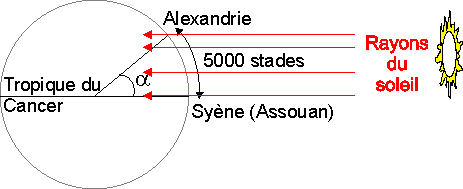
• quatrièmement, - ce qui a été démontré par les géomètres - que les droites qui coupent des parallèles forment (avec elles} des angles alternes égaux.
• cinquièmement, que les arcs qu'interceptent des angles égaux sont semblables, c'est-à-dire qu'ils sont dans la même proportion et dans le même rapport à l'égard des cercles auxquels ils appartiennent. (...)

Celui qui aura maîtrisé ces présupposés comprendra sans difficulté le procédé d'Eratosthène, qui est le suivant. Syène et Alexandrie se trouvent, dit-il, sous le même méridien (céleste}. Puisque les méridiens sont des grands cercles du Monde, il faut nécessairement que leurs projections sur la Terre soient également des grands cercles, de sorte que la 1ongueur que ce procédé établira pour le cercle passant par Syène et Alexandrie sera la longueur du grand cercle de la Terre. Il dit ensuite, - et il en est bien ainsi - que Syène est située sur le cercle tropical d'été (tropique du Cancer).

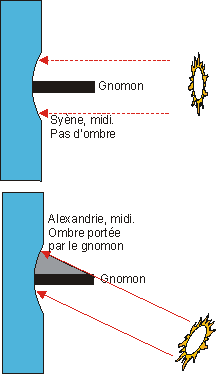
Chaque fois donc que le Soleil, entrant dans le Cancer, culmine dans le Ciel à midi au moment du solstice d'été, nécessairement, les aiguilles des cadrans solaires cessent de porter ombre, du fait que le Soleil les surplombe exactement à la verticale. ... Mais, à Alexandrie à la même heure, les aiguilles des cadrans solaires projettent une ombre, étant donné que cette ville est située plus au nord que Syène. Les deux villes étant situées sous un méridien et sous un grand cercle, si nous traçons à présent, sur le cadran solaire d'Alexandrie, un arc joignant l'extrémité de l'ombre de l'aiguille à la base de celle-ci, cet arc sera une section du grand cercle de la coupe au cadran, puisque cette dernière se trouve sous un grand cercle.

Si ensuite nous imaginons des droites pénétrant dans la Terre depuis chacun des deux cadrans solaires, elles se rencontreront au centre de La Terre. Puisque le cadran solaire de Syène se trouve à la verticale du Soleil, si nous imaginons en outre une droite allant du Soleil au sommet de l'aiguille du cadran, nous obtiendrons une seule droite allant du Soleil au centre de la Terre. Si nous imaginons une autre droite menée depuis la pointe de l'ombre de l'aiguille par la pointe de celle-ci en direction du Soleil à partir de la coupe d'Alexandrie, cette droite et la précédente seront parallèles, dans la mesure où elles joignent des parties différentes du Soleil à des parties différentes de la Terre. Ces droites, qui sont parallèles, sont coupées par la droite joignant le centre de la Terre au cadran solaire d'Alexandrie, de manière à former des angles alternes égaux. L'un d'eux se trouve au centre de la Terre et résulte de l'intersection des droites qui ont été menées depuis les cadrans solaires vers ce centre ; l'autre résulte de l'intersection de l'aiguille du cadran solaire d'Alexandrie et de la droite menée depuis la pointe de son ombre en direction du Soleil en passant par le point de contact avec l'aiguille. Cet angle intercepte l'arc mené de la pointe de l'ombre de l'aiguille à sa base, tandis que celui qui se trouve au centre de la Terre intercepte l'arc joignant Syène à Alexandrie. Ces arcs sont semblables, puisque interceptés par des angles égaux.

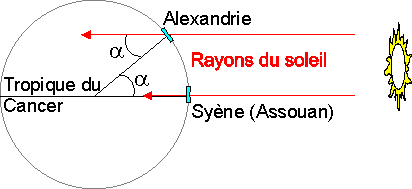
Par conséquent, l'arc contenu dans la coupe sera à l'égard du cercle auquel il appartient dans le même rapport que l'arc joignant Syène à Alexandrie (à l'égard du sien). Or, on trouve que l'arc contenu dans la coupe vaut la cinquantième partie du cercle auquel il appartient. Il faut donc nécessairement que la distance de Syène à Alexandrie soit également la cinquantième partie du grand cercle de la Terre, et cette distance est de cinq mille stades. Par conséquent, le cercle entier mesurera deux cent cinquante mille stades. Tel est le procédé d'Eratosthène.

Commentaires

(Selon GUY DONNAY, A propos de quelques traités d'astronomie traduits en français, dans Grec et Latin en 1981, Etudes et documents, Bruxelles, ULB, Faculté de Philosophie et Lettres, Section de Philologie Classique, 1981, pages 69-70)

• Ce qui compte ici est moins l'exactitude du résultat que l'ingéniosité du procédé. Car :
  • Calcul basé sur des approximations :
    • Syène et Alexandrie ne se trouvent pas sous le même méridien : la différence est d'un peu plus de 3° de longitude, ce qui en fait, n'a aucune incidence sur le résultat, compte tenu de la marge d'approximation.
    • Syène n'est pas exactement sous le Tropique du Cancer, mais environ 1/2° au Nord. Mais les Anciens situaient le Tropique du Cancer à 24° de latitude au lieu de 23° 27'.
    • La distance Alexandrie - Syène est estimée à 5 000 stades soit 1/50ème de cercle (goût des Anciens pour les chiffres ronds).
  • Ignorance actuelle de la longueur du stade utilisé : stade "égyptien" de 157,50 m ? Cette longueur, inventée pour la circonstance n'est pas attestée et reste donc hypothétique.

• Il serait arrivé, selon certaines sources, au résultat de 250 000 stades. D'autres sources parlent de 252 000 stades (252 000 = le nombre rond le plus proche de 250 000 divisible par 360, un degré de latitude valant dès lors 700 stades). Ces nombres correspondent trop à des approximations arrondies pour la facilité des calculs.
• Transposés dans nos mesures modernes, les 252 000 stades, s'ils sont "égyptiens" équivalent à 39 690 km. Ce chiffre, souvent reproduit serait remarquablement proche de la réalité. Mais il est plus que douteux. Pour essayer d'y voir clair :
  • la différence de latitude entre Alexandrie et Syène est d'environ 7° soit pratiquement égale à 1/50ème de la circonférence (7° 12') ;
  • la distance à vol d'oiseau entre ces deux villes est de quelques 790 km, soit à peu de chose près 1/50ème du méridien terrestre (800 km). Cette distance est estimée par Eratosthène à 5 000 stades. Le stade utilisé comme mesure est donc de l'ordre de 160 m. Or un stade de 165 m est attesté à l'époque hellénistique.
  • Sur cette base, on obtient 825 km pour la distance Alexandrie - Syène et 41 250 km pour la circonférence terrestre, soit une erreur par excès de 3%.

2. Posidonius d'Apamée (1er s. avant J.-C.)

Il se base sur l'observation des étoiles pour déterminer la latitude et estimer la circonférence terrestre à quelques 180 000 stades. Cette mesure sera reprise par Ptolémée au 2ème siècle après J.-C. C'est en se basant sur ces mesures que Christophe Colomb imaginera le projet de rejoindre les Indes par l'Ouest. Ce faisant, il sous-estimait le trajet de quelques 10 000 km. Si Ptolémée avait adopté la mesure faite par le savant alexandrin, ERATOSTHÈNE DE CYRÈNE (284-192), peut-être Christophe Colomb ne se serait-il pas lancé dans l'aventure !  

Dernière mise à jour : 11/02/2001 - © Auguste Marchant, 2001